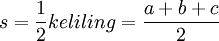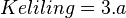Daftar Artikel

  • Tingkatan Bacaan Al Qur'an“Terdapat 4 tingkatan atau mertabat bacaan Al-Quran iaitu bacaan dari segi cepat atau perlahan.
  • Memahami Waktu Shalat Fardhu“Sesungguhnya solat itu diwajibkan atas orang-orang yang beriman menurut waktu-waktu yang tertentu” ( Q.S. An-Nisa’ :103 ) “Dirikanlah solat ketika gelincir matahari hingga waktu gelap malam dan dirikanlah solat subuh sesungguhnya solat subuh itu adalah disaksikan (keistimewaannya)”. ( Q.S. Al-Isra’ : 78 )
  • Sesuatu yang tidak dimiliki ALLAH SWTSuatu hari Anas bin Malik menyaksikan seorang Yahudi yang datang menghadap Khalifah Abu Bakar dan berkata, “Aku ingin bertemu dengan khalifah Rasulullah saw.” Para sahabat membawanya kepada Khalifah Abu Bakar. Dihadapan Abu Bakar, orang Yahudi berkata, “Anda khalifah Rasulullah saw?”...
  • Cinta Allah dan Rasulullah Allah Swt berfirman, "katakanlah, jika kalian (benar-benar) mencintai Allah, ikutilah aku, niscya Allah mengasihi kalian" (QS Ali `Imran [3]:31).
  • Malu Sebagian Dari Iman عَنْ أَبِي مَسْعُوْدٍ عُقْبَةَ بِنْ عَمْرٍو الأَنْصَارِي الْبَدْرِي رَضِيَ الله عَنْهُ قَالَ : قَالَ رَسُوْلُ اللهِ صَلَّى اللهُ عَلَيْهِ وَسَلَّمَ : إِنَّ مِمَّا أَدْرَكَ النَّاسُ مِنْ كَلاَمِ النُّبُوَّةِ الأُوْلَى، إِذَا لَمْ تَسْتَحِ فَاصْنَعْ مَا شِئْتَ [رواه البخاري ] Dari Abu Mas’ud ‘Uqbah bin ‘Amr Al Anshari Al Badri radhiyallahu’anhu, Nabi shallallahu ‘alaihi wasallam bersabda, “Sesungguhnya di antara ucapan kenabian yang pertama kali ditemui manusia...
  • Makna Sabar Dari Suhaib ra, bahwa Rasulullah SAW bersabda, "Sungguh menakjubkan perkaranya orang yang beriman, karena segala urusannya adalah baik baginya. Dan hal yang demikian itu tidak akan terdapat kecuali hanya pada orang mu'min: Yaitu jika ia mendapatkan kebahagiaan, ia bersyukur, karena (ia mengetahui) bahwa hal tersebut merupakan yang terbaik untuknya. Dan jika ia tertimpa musibah, ia bersabar, karena....
  • Mimpi sebuah keindahan hidup semua orang disekeliling kita pasti pernah mengalami mimpi, entah itu mimpi yang baik maupun yang buruk. Apakah Mimpi itu ? Habib Asseggaf dalam ungkapan filosofisnya pernah menuturkan "Mimpi yang baik itu adalah keindahan dalam hidup." mimpi juga pernah dialami oleh para nabi dan...
  • Menipiskan Alis Salah satu cara berhias yang berlebih-lebihan yang diharamkan Islam, yaitu mencukur rambut alis mata untuk ditinggikan atau disamakan. Dalam hal ini Rasulullah pernah melaknatnya, seperti tersebut dalam hadis:.....
  • Menyambung Rambut Termasuk perhiasan perempuan yang terlarang ialah menyambung rambut dengan rambut lain, baik rambut itu asli atau imitasi seperti yang terkenal sekarang ini dengan nama wig....
  • Semir Rambut Sehubungan dengan masalah ini ada satu riwayat yang menerangkan, bahwa orang-orang Yahudi dan Nasrani tidak memperkenankan menyemir rambut dan merombaknya, dengan.....
  • Jiwa Yang Tenang Jiwa yang tenang itu berangkat dari kebaikan dan selalu memperlihatkan gejala-gejala yang normal. ia selamanya bertawakal kepada ALLAH, rela menerima rizki yang baik maupun yang Jelek, berjuang, konsisten terhadap kebenaran, tidak pernah mengeluh dikala mengalami cobaan dan malapetaka....
  • Ciri-Ciri Wanita Sholehah Tidak banyak syarat yang dikenakan oleh Islam untuk seseorang wanita untuk menerima gelar solehah, dan seterusnya menerima pahala syurga yang penuh kenikmatan dari Allah SWT.....
  • Memelihara Jenggot Termasuk yang urgen dalam permasalahan kita ini, ialah tentang memelihara jenggot. Untuk ini Ibnu Umar telah meriwayatkan dari Nabi s.a.w. yang mengatakan sebagai berikut:....

    • Rumus Segitiga



    Segitiga atau segi tiga adalah nama suatu bentuk yang dibuat dari tiga sisi yang berupa garis lurus dan tiga sudut. Matematikawan Euclid yang hidup sekitar tahun 300 SM menemukan bahwa jumlah ketiga sudut di suatu segi tiga adalah 180 derajat. Hal ini memungkinkan kita menghitung besarnya salah satu sudut bila dua sudut lainnya sudah diketahui.





    Klasifikasi segitiga

    Menurut panjang sisinya:
    • Segitiga sama sisi adalah segitiga yang ketiga sisinya sama panjang. Sebagai akibatnya semua sudutnya juga sama besar, yaitu 60o.
    • Segitiga sama kaki adalah segitiga yang dua dari tiga sisinya sama panjang. Segitiga ini memiliki dua sudut yang sama besar.
    • Segitiga sembarang adalah segitiga yang ketiga sisinya berbeda panjangnya. Besar semua sudutnya juga berbeda.
    Equilateral Triangle Isosceles triangle Scalene triangle
    Segitiga sama sisi Segitiga sama kaki Segitiga sembarang

    Menurut besar sudut terbesarnya:
    • Segitiga siku-siku adalah segitiga yang besar sudut terbesarnya sama dengan 90o. Sisi di depan sudut 90o disebut hipotenusa atau sisi miring.
    • Segitiga lancip adalah segitiga yang besar sudut terbesarnya < 90o
    • Segitiga tumpul adalah segitiga yang besar sudut terbesarnya > 90o
    Right triangle Obtuse triangle Acute triangle
    Segitiga siku-siku Segitiga tumpul Segitiga lancip


    Mencari luas dan keliling segitiga

    • Luas = \frac{alas.tinggi}{2}\,
    • Keliling = sisi1 + sisi2 + sisi3\,
    Teorema Heron
    Teorema Heron biasanya digunakan untuk mencari luas dari suatu segitiga sembarang. a, b dan c adalah ketiga sisi segitiga.
    • s = \frac{1}{2} keliling = \frac{a+b+c}{2}\,
    • Luas = \sqrt{s(s-a)(s-b)(s-c)}\,
    Segitiga sama sisi
    Untuk mencari luas dan keliling segitiga sama sisi yang bersisi a dapat digunakan rumus sebagai berikut:
    • Luas = \frac{a^2}{4} \sqrt{3}\,
    • Keliling = 3.a\,

    Dalil Pythagoras


    Segitiga siku-siku

    Dalil Pythagoras hanya berlaku pada segitiga siku-siku. Pythagoras menyatakan bahwa: c^2 = a^2 + b^2\,
    Jika ada tiga buah bilangan a, b dan c yang memenuhi persamaan di atas, maka ketiga bilangan tersebut disebut sebagai Triple Pythagoras. Triple Pythagoras tersebut dapat dibangun menggunakan rumus berikut dengan memasukkan sebuah nilai n dengan n adalah bilangan bulat positif.
    Labels:

    Powered byEMF Forms Online
    Report Abuse